Metoda obliczeń
Rozmiar układu
Makroskopowy kryształ składa się z >1024 cząstek. Wykonanie obliczeń dla rzeczywistego układu wymagałoby wielokrotnego rozwiązywania układu >1024 równań ruchu. Takie zadanie jest mało realne ze względu na czas obliczeń. Dlatego do obliczeń przyjmujemy układ znacznie mniejszy. Zazwyczaj jest to krystalit składający się z kilku tysięcy atomów. Wielkość krystalitu należy tak określić, aby otrzymywane wyniki nie zależały od rozmiaru badanego układu.
Numeryczne rozwiązywanie równań ruchu
Obliczanie położeń
Znając położenia cząstek w chwili t xi(t) możemy obliczyć położenia cząstek w chwili t+dt z następującego wzoru:
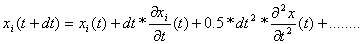
gdzie 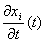 - prędkość cząstki i w chwili t, a - przyspieszenie cząstki w chwili t. Korzystając z równań ruchu Newtona
- prędkość cząstki i w chwili t, a - przyspieszenie cząstki w chwili t. Korzystając z równań ruchu Newtona 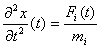 . Wyrazy wyższych rzędów we wzorze na położenie można by zaniedbać, gdyby siła F była stała. W większości przypadków tak nie jest. Jedną z metod przybliżonego uwzględnienia tego faktu jest tzw. metoda stałej siły.
. Wyrazy wyższych rzędów we wzorze na położenie można by zaniedbać, gdyby siła F była stała. W większości przypadków tak nie jest. Jedną z metod przybliżonego uwzględnienia tego faktu jest tzw. metoda stałej siły.
Metoda średniej siły
Metoda stałej siły składa się z następujących kroków:
- stosując poniższy wzór liczymy położenia cząstek w chwili t+dt:
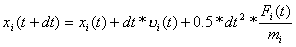
Otrzymane położenia są niedokładne bo zaniedbaliśmy wyrazy wyższych rzędów. - liczymy siłę działającą na cząstkę i w chwili t+dt wywieraną przez wszystkie pozostałe cząstki Fi (t+dt);
- liczymy średnią siłę
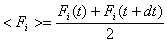
- liczymy nowe położenia cząstek w chwili t+dt podlegających działaniu siły <Fi>
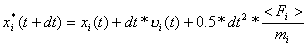 dla i=1,N.
dla i=1,N.
Powyższa metoda jest dokładniejsza niż metoda, w której zatrzymalibyśmy się na kroku 1 ponieważ uwzględnia zmianę siły ze zmianą konfiguracji układu (czasem). Końcowe położenia x*i są tym bardziej zbliżone do rzeczywistych im mniejsza jest zmiana siły. W obliczeniach zwykle zakłada się jakąś wartość maksymalnie dopuszczalnej zmiany siły Fo. Jeżeli siła zmienia się w danym kroku iteracyjnym o więcej niż Fo to należy zmniejszyć krok czasowy dt i powtórzyć wszystkie obliczenia.
Algorytm używany w naszym przypadku jest bardziej złożony. Jest on oparty o metodę fifth-gear predictor-corector uwzględniającą rozwinięcie szeregu Tylora do piątego rzędu.
Krok czasowy obliczeń dt nie jest więc stały. Jeżeli w danym momencie siły są słabo zależne od czasu dt może być duże. Jednak, jeżeli siły silnie zmieniają się z czasem dt musi ulec zmniejszeniu. Typowy krok czasowy wynosi dziesiąte części femtosekundy (1 fs = 10-15 s).
Obliczanie sił
Siłę Fi obliczamy ze znajomości potencjałów oddziaływania cząstek Vi(x) z następującego wzoru: 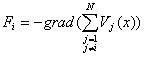 , gdzie sumowanie j rozciąga się po wszystkich cząstkach badanego układu z wyjątkiem cząstki i, dla której liczymy siłę.
, gdzie sumowanie j rozciąga się po wszystkich cząstkach badanego układu z wyjątkiem cząstki i, dla której liczymy siłę.
Podstawowym elementem symulacji komputerowych jest więc znajomość potencjałów oddziaływania. Na szczęście potencjały te są już znane dla większości interesujących układów.
Zasięg oddziaływania
Większość ze stosowanych potencjałów oddziaływania cząstek jest krótkozasięgowa. W rezultacie mało ekonomiczne byłoby obliczanie oddziaływania danej cząstki z cząstkami znajdującymi się w odległości większej niż zasięg oddziaływania R. Aby zwiększyć szybkość obliczeń wprowadza się pojęcie bliskich sąsiadów, tj. cząstek znajdujących się w odległości mniejszej niż R. Tylko te cząstki są uwzględniane w obliczeniach oddziaływań. Liczba bliskich sąsiadów wynosi zwykle kilkadziesiąt cząstek.
Przykładowa zależność energii potencjalnej od odległości międzyatomowej.
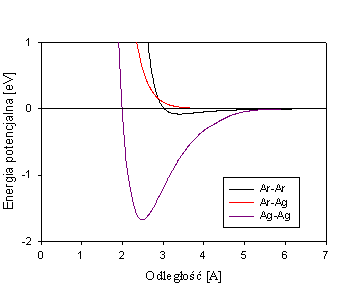
Granica zasięgu potencjału R = ~ 1 nm

